主要内容:路径追踪、重要性采样、不同光学模型材料、布料仿真、材质、抗锯齿
概览
实现功能
基础功能:
-
基于硬件的路径追踪算法
-
通过硬件渲染器增加一个传入参数:所有光源的 idx,实现直接对光采样,效率迅速提升
-
实现了理想镜面 Specular 和理想折射体 Transmissive,并可在Gui界面中直接调节材料的折射率
-
利用 Phong 模型的 BRDF,实现有光泽材质 Principled
拓展功能:
-
实现 Lambertian 和 Phong 模型材料的余弦重要性抽样
-
利用微表面模型和GGX分布实现了一种可调节折射率$\eta$和粗糙程度$\alpha$的透明材质,并实现了基于BRDF(BTDF)函数的重要性抽样
-
使用质点-弹簧模型,完成了一个布料仿真程序,并将布料放置在了场景内
-
为场景中的一些物体定义了uv坐标,贴上了(经过自己缝合的)Minecraft原版材质包
渲染结果展示
(1)实现直接光源采样前后的渲染速度对比:左边为无光源采样时长时间迭代的效果,右边为有直接光源采样经过短时间运行的效果。
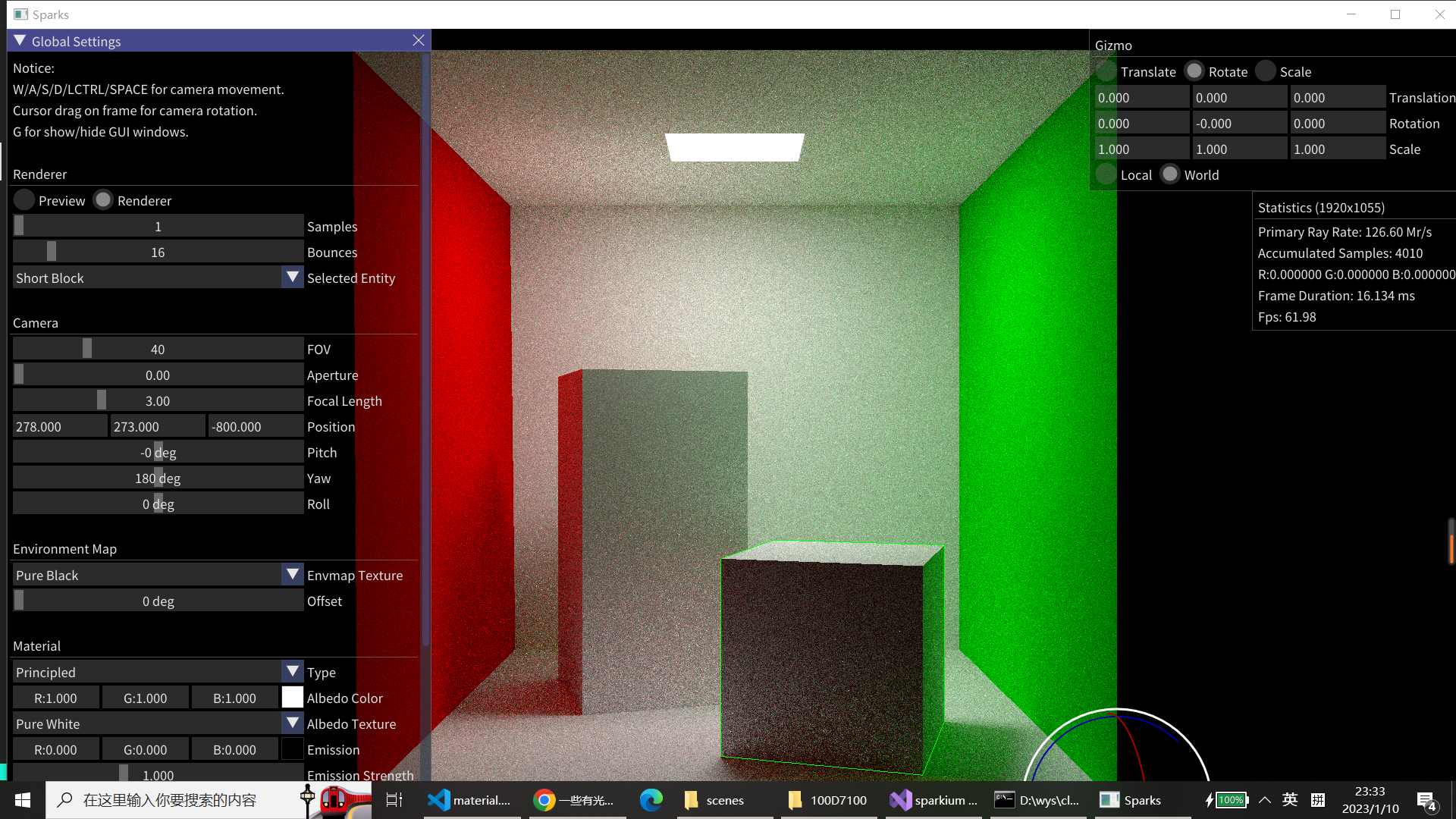
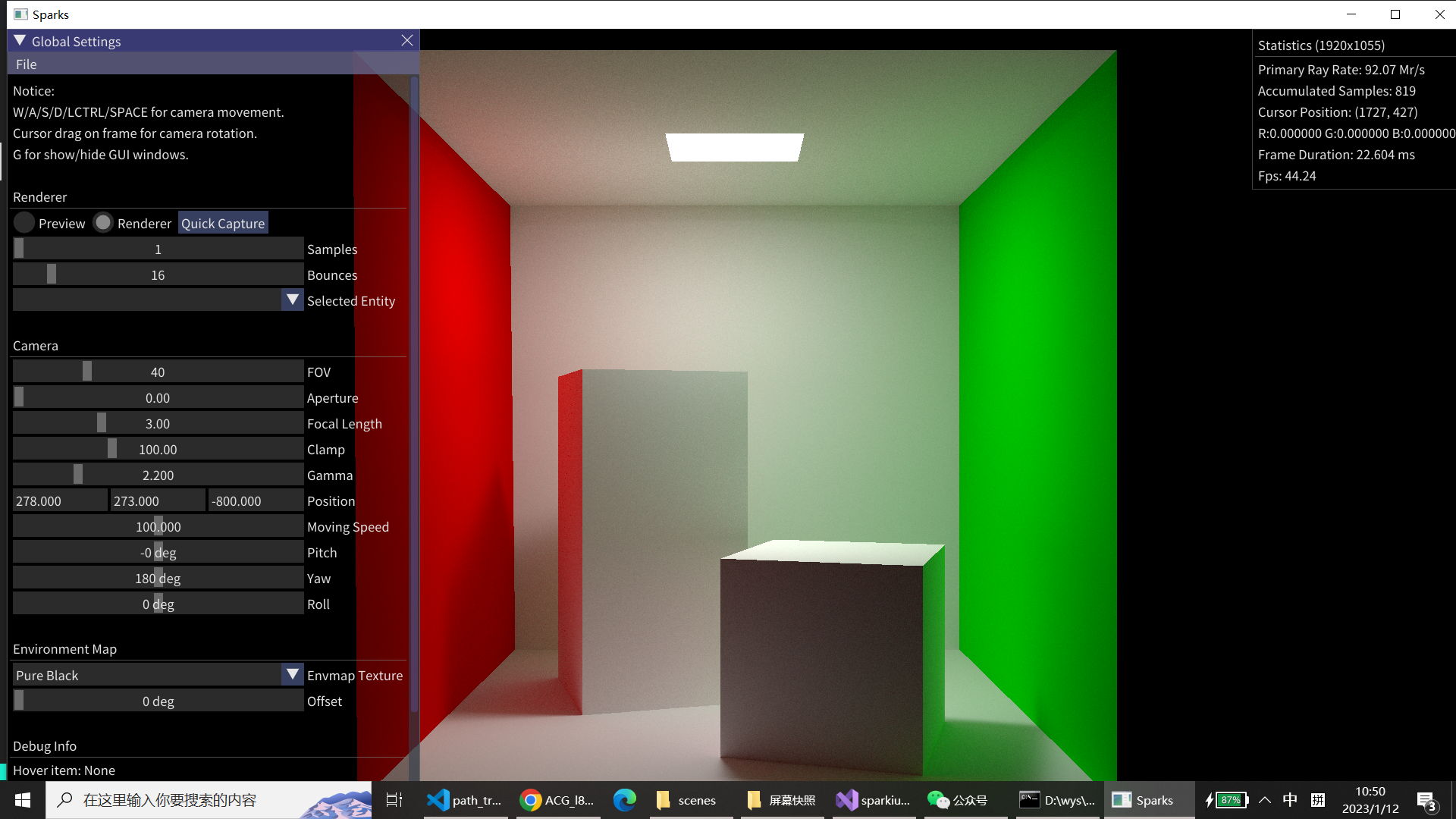
(2)经过修补前后的直接光源采样效果:可见左上角光斑有所变化
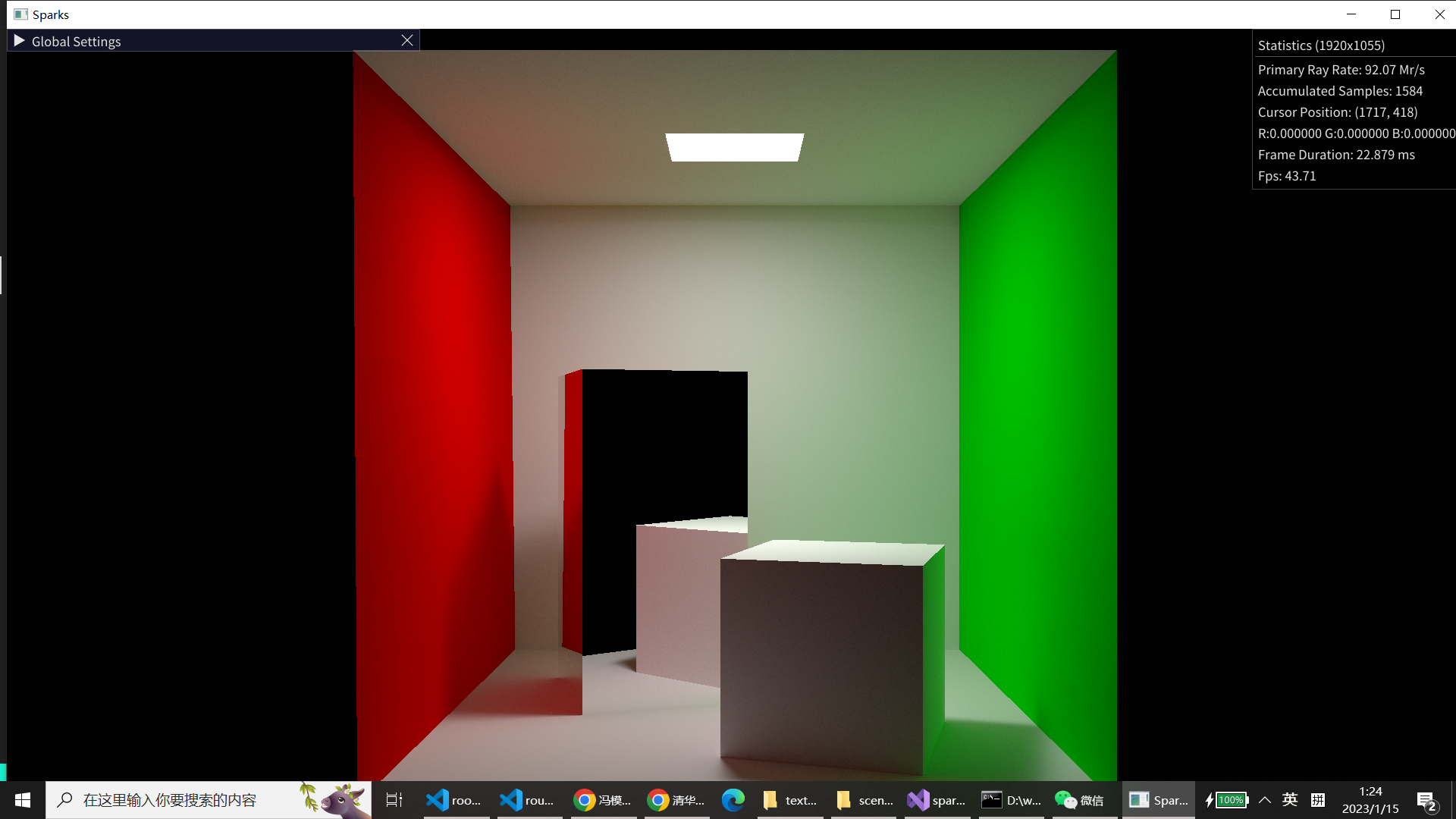
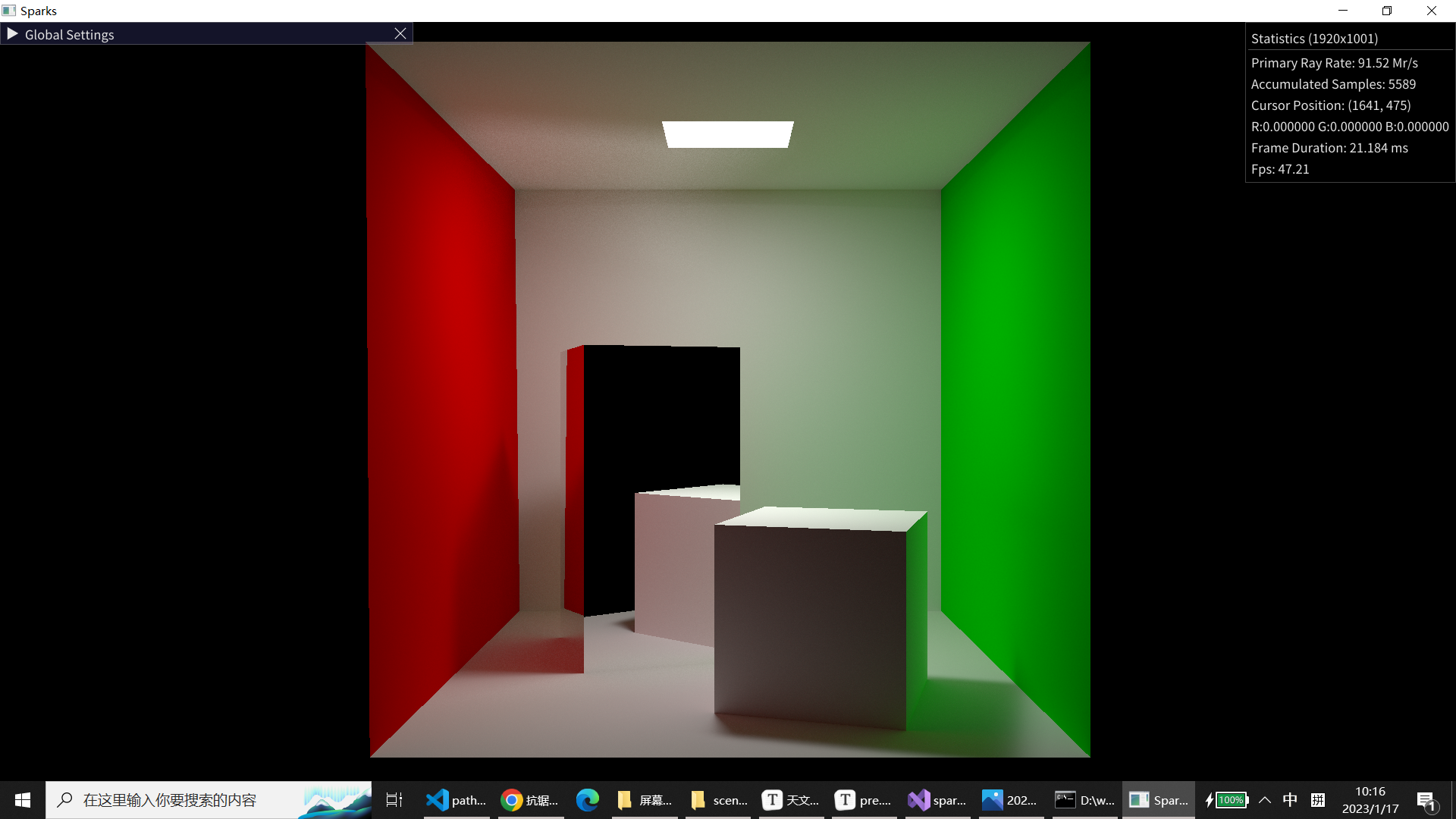
(3)根据微表面模型实现的投射材料,在不同$\alpha$值(从0到1)下的表现情况
.png)
.png)
.png)
.png)
(4)几个不同颜色、不同折射率、不同$\alpha$值透射材料放在一起的综合表现情况:
.png)
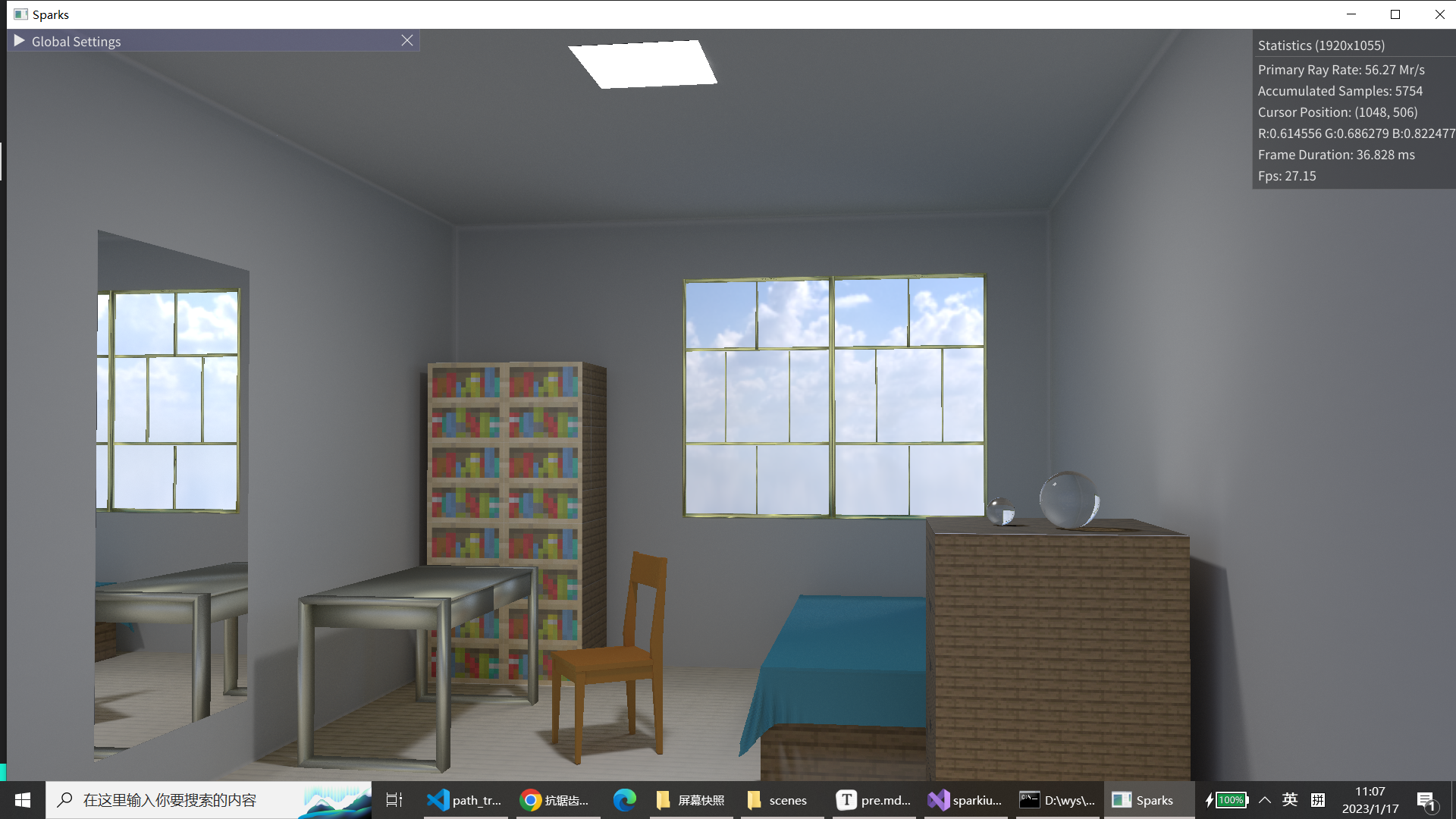
(5)自定义场景:温馨房间
功能实现方法
路径追踪与直接光源采样
包括直接光源采样的路径追踪方法如下:
vec3 SampleRay(vec3 origin, vec3 direction) {
vec3 radiance = vec3(0.0);
vec3 throughput = vec3(1.0);
float rr_prob = 0.85;
int diffusive = 0; // record of diffusive surface
while (true) {
TraceRay(origin, direction);
if (ray_payload.t == -1.0) { // not hit
radiance += throughput * SampleEnvmap(direction);
break;
}
Material material = materials[hit_record.hit_entity_id];
if (material.material_type is not diffusive) {
// Sample a point on an emission entity
// Trace a ray towards the direction of the point
if (/*There is no obstacle*/) {
vec3 radiance_dir = material0.emission * material0.emission_strength * INV_PI / 2
* bsdf(material, direction0, direction, hit_record.normal)
* dot(normalize(hit_record.normal), direction0)
* dot(normal0, -direction0)
/ pow(length(hit_record0.position-hit_record.position),2)
* ls_cnt * area * light_sources[1];
radiance += throughput * material.albedo_color * radiance_dir;
}
}
if (fract(RandomFloat()) > rr_prob)
break;
throughput /= rr_prob;
if (material.material_type == EMISSION) {
if (diffusive == 0)
radiance += throughput * material.emission * material.emission_strength;
break;
}
else {
// dealing with different materials
if (material.material_type is diffusive)
diffusive = 1;
else
diffusive = 0;
}
Phong模型的BRDF
Phong模型定义的BRDF如下:
\[f_r(x,\omega_i, \omega_o) = \frac{f_d}{\pi} + \frac{(n+2)k_s}{2\pi} [\max(0,\cos\alpha)]^n\] // Phong model
float kd = 0.2; // fraction of diffuse reflectivity
float ks = 1-kd; // fraction of specular reflectivity
int n = 8; // specular exponent
vec3 median = -dot(in_direction, normal_direction) * normal_direction;
vec3 spe_out_direction = 2*median + in_direction;
float cosine = max(0,dot(out_direction, spe_out_direction));
float t1 = kd * INV_PI;
float t2 = ks * (n+2) * INV_PI / 2 * pow(cosine,n);
return vec3(t1+t2) * material.albedo_color;
遵循微表面模型和GGX分布的透射体
微表面模型定义的BRDF如下:
\(f_r(x,\omega_i, \omega_o) = \frac{F(\omega_i, h) G(\omega_i, \omega_o, h)D(h)}{4|\omega_i \cdot n|\ |\omega_o\cdot n|}\) 其中F为菲涅尔项,D为微表面分布函数,G为阴影遮蔽函数。在GGX分布下,D和G的定义分别如下:
\[D(\omega) = \frac{\alpha^2}{\pi [(\alpha^2-1)\cos^2\left<\omega,n\right> + 1]^2} \\ G(\omega_i,\omega_o,m) = G_1(\omega_i,m)G_1(\omega_o,m), G_1(\omega,m) = \frac{2\chi^+((\omega\cdot m)(\omega\cdot n))}{1+\sqrt{1+\alpha^2\tan\left<v,n\right>}}\]float Fresnel_term(vec3 in_direction, vec3 half_direction, float eta) {
float fresnel;
float c = abs(dot(in_direction, half_direction));
float gsquare = c*c - 1 + eta*eta;
if (gsquare > 0) {
float g = sqrt(gsquare);
fresnel = 0.5 * (g-c) * (g-c) / (g+c) / (g+c) * (1 + (c*g + c*c -1) * (c*g + c*c - 1) / (c*g - c*c + 1) / (c*g - c*c + 1));
} else {
fresnel = 1;
}
return fresnel;
}
float Microfacet_pdf_term(vec3 half_direction, vec3 normal_direction, float alpha) {
float microfacet_pdf;
float cos_theta_mn = dot(half_direction, normal_direction);
if (cos_theta_mn > 0)
microfacet_pdf = alpha * alpha *INV_PI / pow(cos_theta_mn, 4) / pow((alpha*alpha - 1 + 1 / cos_theta_mn / cos_theta_mn),2);
else
microfacet_pdf = 0;
return microfacet_pdf;
}
float Shadow_term(vec3 in_direction, vec3 out_direction, vec3 normal_direction, vec3 half_direction, float alpha) {
float cos_theta_in = dot(-in_direction, normal_direction);
float cos_theta_on = dot(out_direction, normal_direction);
float cos_theta_im = dot(-in_direction, half_direction);
float cos_theta_om = dot(out_direction, half_direction);
float g1;
if (cos_theta_im * cos_theta_in > 0)
g1 = 2 / (1+sqrt(1 + alpha*alpha * (1/cos_theta_in/cos_theta_in - 1)));
else
g1 = 0;
float g2;
if (cos_theta_om * cos_theta_on > 0)
g2 = 2 / (1+sqrt(1 + alpha*alpha * (1/cos_theta_on/cos_theta_on - 1)));
else
g2 = 0;
float shadow = g1*g2;
return shadow;
}
具体的取样方式在下两小节介绍。
余弦权重重要性采样
余弦权重重要性采样,也就是概率密度函数与出射方向和法线方向夹角的余弦成正比,即
\(p(\theta,\phi) = \frac{\cos\theta \sin\theta}{\pi}\) 由独立的$\xi_1,\xi_2\sim U[0,1]$,我们可以得到采样:
\[\theta = \arccos\sqrt{1-\xi_1}, \phi = 2\pi \xi_2\]BRDF权重的重要性采样
BRDF权重重要性采样,也就是概率密度函数与BRDF/BSDF函数成正比。当我们使用GGX分布函数时,采样方法主要分为如下三步:
1. 采样一个微表面法向量
由两个$U[0,1]$的独立随机变量$\xi_1,\xi_2$,我们按以下方式采样的法方向满足GGX分布:
\(\theta_m = \arctan (\alpha \sqrt{\xi/(1-\xi)}), \phi_m = 2\pi\xi_2\) 从宏观表面法向量$n$,利用$\theta,\phi$做变换即可得到微表面法向量$m$。
float eta = material.transmissive_ratio;
float alpha = material.alpha;
float rand1 = fract(RandomFloat());
float rand2 = fract(RandomFloat());
// sample the microfacet normal
float theta = atan(alpha * sqrt(rand1 / (1-rand1)));
float phi = 2*PI*rand2;
vec3 local_z = -sign(dot(direction, hit_record.normal))*normalize(hit_record.normal);
vec3 local_x = normalize(direction - dot(direction, local_z) * local_z);
vec3 local_y = cross(local_z,local_x);
vec3 half_direction = normalize(sin(theta)*cos(phi)*local_x + sin(theta)*sin(phi)*local_y + cos(theta)*local_z);
2. 计算Fresnel项,决定折射或者反射
利用2.3节中的公式,我们可以计算Fresnel项的值$F$。之后在$U[0,1]$中随机抽取一个随机变量$\xi_3$,若$\xi_3\le F$则为反射,否则为折射,并根据微表面法线方向,利用完美反射/折射公式计算出出射光线的方向.
float fresnel = Fresnel_term(direction, half_direction, eta);
if (fract(RandomFloat()) < fresnel) {
// reflective
out_direction = 2 * dot(-direction, half_direction) * half_direction + direction;
} else {
// transmissive
float c = dot(-direction, half_direction);
out_direction = (c/eta - sign(dot(-direction, hit_record.normal)) * sqrt(1 + (c*c-1)/eta))
* half_direction + direction / eta;
}
3. 计算对应方向权重
为这一方向计算光线权重,并处理throughput等迭代相关信息:
\[W(\omega_o) = G(\omega_i,\omega_o,n) \frac{\omega_i\cdot m}{(\omega_i\cdot n)(m\cdot n)}\]float weight = dot(-direction, half_direction) / dot(-direction, hit_record.normal)
dot(half_direction, hit_record.normal) * Shadow_term(direction, out_direction,
hit_record.normal, half_direction, alpha);
throughput *= (material.albedo_color *
vec3(texture(texture_samplers[material.albedo_texture_id],hit_record.tex_coord)) * weight);
origin = hit_record.position;
direction = out_direction;
布料模拟
为了做出场景中床单的效果,单独做了一个使用质点-弹簧模型的布料模拟程序。每个质点连接其周围八个质点,以及相距为2的四个质点,每个时间步长内计算其受力、加速度、速度以及位移。
void evolve(float dt, float hook) {
for (int i = 0; i < position_.size(); i++) {
float supporting_force = 0;
if (supporting_x[0] <= position_[i].x && position_[i].x <= supporting_x[1] &&
supporting_z[0] <= position_[i].z && position_[i].z <= supporting_z[1] &&
position_[i].y <= supporting_y[1] + 0.2f &&
position_[i].y >= supporting_y[1] - 0.2f && force_[i].y < 0) {
// if on the bedboard, add supporting force and friction
supporting_force = -force_[i].y;
force_[i].y = 0;
velocity_[i].y = 0;
if (length(velocity_[i]) == 0) {
if (length(force_[i]) <= frac_coeff * supporting_force) {
force_[i] = vec3{0.0f};
} else {
force_[i] -= frac_coeff * supporting_force * normalize(force_[i]);
}
} else {
force_[i] -= frac_coeff * supporting_force * normalize(velocity_[i]);
}
}
// dealing with collision
if (supporting_x[0] <= position_[i].x && position_[i].x <= supporting_x[1] &&
supporting_y[0] <= position_[i].y && position_[i].y <= supporting_y[1] &&
position_[i].z <= supporting_z[0] + 10.0f &&
position_[i].z >= supporting_z[0] - 0.02f && velocity_[i].z > 0)
velocity_[i].z = 0.0f;
if (supporting_x[0] <= position_[i].x && position_[i].x <= supporting_x[1] &&
supporting_y[0] <= position_[i].y && position_[i].y <= supporting_y[1] &&
position_[i].z <= supporting_z[1] + 0.02f &&
position_[i].z >= supporting_z[1] - 10.0f && velocity_[i].z < 0)
velocity_[i].z = 0.0f;
if (supporting_z[0] <= position_[i].z && position_[i].z <= supporting_z[1] &&
supporting_y[0] <= position_[i].y && position_[i].y <= supporting_y[1] &&
position_[i].x <= supporting_x[0] + 10.0f &&
position_[i].x >= supporting_x[0] - 0.02f && velocity_[i].x > 0)
velocity_[i].x = 0.0f;
if (supporting_z[0] <= position_[i].z && position_[i].z <= supporting_z[1] &&
supporting_y[0] <= position_[i].y && position_[i].y <= supporting_y[1] &&
position_[i].x <= supporting_x[1] + 0.2f &&
position_[i].x >= supporting_x[1] - 10.0f && velocity_[i].x < 0)
velocity_[i].x = 0.0f;
position_[i] += dt * velocity_[i];
velocity_[i] *= damp_factor;
velocity_[i] += dt * force_[i];
force_[i] = vec3{0.0f, -9.8f, 0.0f};
}
for (int i = 0; i < springs_.size(); i++) {
vec3 vec0to1 = -position_[springs_[i][0]] + position_[springs_[i][1]];
float length = glm::length(vec0to1);
vec3 force = hook * (length - o_length[i]) * glm::normalize(vec0to1);
force_[springs_[i][0]] += force / mass;
force_[springs_[i][1]] -= force / mass;
}
}
抗锯齿
在每个像素内的区域内随机采样十个点,计算其RGB值平均作为这个像素点的采样。
Credits and References
Besides the slides in class, I’ve also refered to the materials below for counterparts of the project:
-
Naive path tracing: https://zhuanlan.zhihu.com/p/475547095.
-
Directly sampling the light https://zhuanlan.zhihu.com/p/475547095.
-
Principled material in Phong model BRDF: https://zhuanlan.zhihu.com/p/500811555.
-
Cosine importance sampling: https://zhuanlan.zhihu.com/p/360420413.
-
Principled/transmissive material in microfacet model:
-
Bruce Walter, Stephen R. Marschner, Hongsong Li, and Kenneth E. Torrance. 2007. Microfacet models for refraction through rough surfaces. In Proceedings of the 18th Eurographics conference on Rendering Techniques (EGSR’07). Eurographics Association, Goslar, DEU, 195-206.
-
The mitsuba project: https://github.com/mitsuba-renderer/mitsuba.
-
Textures: adapted from the Minecraft game sources.