2022春数学系《概率论1》笔记,教师:荆文甲
Notes of DMS Probability I course, Spring 2022, taught by Prof. Wenjia Jing.
Chapter 3: Independence and Convergence by distribution
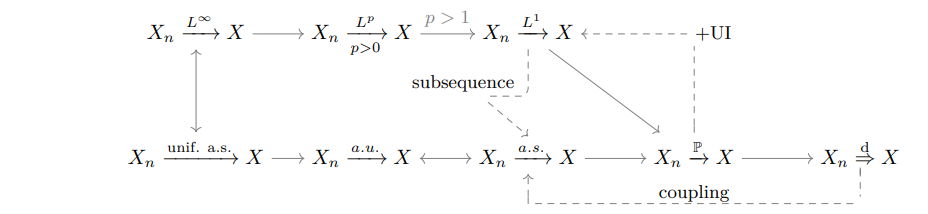
Chapter 4: LLN
假设$\{X_n\}$ i.i.d., 有以下的大数定律成立:
- (Chebyshev WLLN) $X_1\in L^2(\Omega)$, 则 $\frac{S_n}{n} \to m$ 依$L^2$范数收敛, 从而依概率收敛;
- (Markov SLLN) $X_1\in L^4(\Omega)$, 则 $\frac{S_n}{n} \to m$ 几乎处处收敛.
- (KhinChin WLLN) $X_1 \in L^1(\Omega)$, 则 $\frac{S_n}{n} \to m$ 依概率收敛. (proof. 截断法)
- (Komogorov SLLN) $X_1 \in L^1(\Omega)$, 则 $\frac{S_n}{n} \to m$ 几乎处处收敛.

Chapter 5: CLT
Def. (Characteristic function) $\hat \mu (t) = \int_\mathbb{R} e^{itx} d\mu(x) = \mathbb{E}[e^{itX}]$ for $X\sim \mu$. 若$X$绝对连续, 则这就是对pdf的Fourier变换.
Prop. $\phi_\mu(0) = 1$, $\lvert \phi_\mu(t)\rvert \le 1$, $\phi_{\mu}(t) = \overline{\phi_{\mu(-t)}}$, $\phi_{aX+b}(t)= e^{itb}\phi_X(at)$; $\phi_\mu: \mathbb{R} \to \mathbb{C}$ is uniformly continuous; The convex combination of c.f.s is also a c.f.; If $X\perp Y$, then $\phi_{X+Y} = \phi_X\phi_Y$.

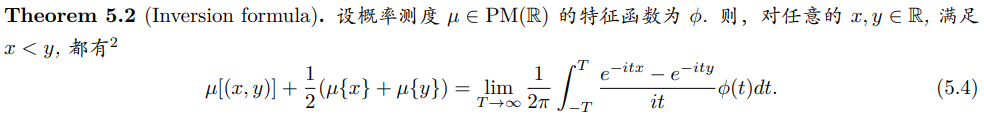
由此可反向由特征函数唯一确定一个概率分布.
特征函数与概率测度的弱收敛
Prop. $\mu_n,\mu\in PM(\mathbb{R})$, $\mu_n \Rightarrow \mu$, 则$\phi_n(t)$在$\mathbb{R}$上一致等度连续, 且$\phi_n$局部一致收敛到$\phi$(在任意紧集上一致收敛).
Thm. 对$\mu_n\in PM(\mathbb{R})$, 若$\phi_n(x) \to \phi(x),\forall x \in\mathbb{R}$, 且极限函数$\phi$在$0$处连续, 则$\phi$是一个概率测度$\mu$的特征函数, 且$\mu_n\Rightarrow \mu$.
Prop. (Moments)
- 若$\mu$有$m$阶矩, 则$\phi\in C^m(\mathbb{R})$ 且 $\phi^{(m)}(t) = \int_\mathbb{R} (ix)^m e^{itx} d\mu(x).$
- 若$\phi^{(m)}(0)$对某个偶数$m$存在, 则$\phi$在$0$处有$m$阶导数, 且$\mu$有$m$阶矩, 可通过以上公式计算.
中心极限定理
Thm. (初等CLT) $\{ X_j \}$ iid, 且 $X_1\in L^2$, 则 $\frac{S_n - \mathbb{E}[S_n]}{\sqrt{n\sigma^2}} \Rightarrow^d \chi \sim N(0,1)$.
Thm. (Lyapunov) $X_n$ 独立, $\mathbb{E}[X_n] = 0$, $\sigma_n^2 = \text{Var}[X_n]$, $\alpha_n^2 = \text{Var}[S_n] = \sum_{j=1}^n\sigma_j^2$. 若 \(\{X_n\}_{n\in\mathbb{N}} \subset L^3(\Omega),\) 且 \(\lim_{n\to\infty}\frac{\sum \mathbb{E}[\lvert X_j\rvert^3]}{\alpha_n^3} = 0,\) 则
\[\frac{S_n}{\alpha_n} = \frac{S_n}{\sqrt{\text{var}S_n}} \Rightarrow N(0,1).\]Thm. (Lindeberg-Feller) 若对于每个$n$, \(\{ X_{n,m} \}_{1< m< n}\) 独立, 且均值为零。设 \(S_n^\sharp = \sum_{m=1}^n X_{m,n}, \alpha_n^2 = \sum^n_{m=1} \sigma^2_{n,m}.\) 若
- Normalized: $\alpha^2 = \sum_{m=1}^n \sigma_{n,m}^2 = 1$
- Linderberg-Feller condition: $\forall \varepsilon > 0$, \(\lim_{n\to \infty}\sum_{m=1}^n \mathbb{E}[\lvert X_{n,m}\rvert^2 \mathbf{1}_{\lvert X_{n,m}\rvert >\varepsilon} ] = 0.\)
则我们有 \(S_n^\# \Rightarrow N(0,1).\)
Poisson极限定理
若对于每个$n$, \(\{X_{n,m}\}_{1\le m\le n}\) 独立, 且满足Bernoulli分布 \(\mathbb{P}[X_{n,m}= 1] =p_{n,m}.\) 记 \(S_n^\# = \sum_{m=1}^nX_{m,n},\) 若
\[\lim_{n\to\infty}\sum_{m=1}^n p_{n,m} = \lambda > 0, \lim_{n\to\infty}\max_{1\le m\le n} p_{n,m} = \lambda > 0,\]则 \(S_n^\# \Rightarrow \text{Poisson}(\lambda).\)
Chapter 6: Conditional Expectation & Martingale
Def. (Conditional Expectation) $X\in L^1(\Omega, F, \mathbb{P})$, $\mathcal{A} \subset F$ is a sub $\sigma$-algebra, then $\mathbb{E}[X \vert A]$ is defined as a random variable $Y$ measurable on $\mathcal{A}$ s.t. $\mathbb{E}[X\mathbb{1}_A] = \mathbb{E}[Y\mathbb{1}_A]$.
存在性、唯一性、线性性质、保号性、单调性. 重要性质:
- (MCT) $X_n \ge 0$ a.s., $X_n \uparrow X\in L$, then $\mathbb{E}[X\vert\mathcal{A}] = \lim_{n\to \infty}\mathbb{E}[X_n \vert \mathcal{A}]$.
- (Fatou) $X_n \ge 0$ a.s., then $\mathbb{E}[\liminf_{n\to \infty} X\vert\mathcal{A}] \le \liminf_{n\to \infty}\mathbb{E}[X_n \vert\mathcal{A}]$.
- (DCT) $\lvert X_n\rvert \le Z \in L^1$, $X_n \to X$ a.s, then $\mathbb{E}[X\vert \mathcal{A}] = \lim_{n\to \infty} \mathbb{E}[X_n \vert \mathcal{A}]$.
- (Towering) $\mathcal{B}\subset \mathcal{A} \subset F$, then $\mathbb{E}[ \mathbb{E}[X\vert \mathcal{A}]\vert \mathcal{B}] = \mathbb{E}[ \mathbb{E}[X\vert\mathcal{B}]\vert\mathcal{A}] = \mathbb{E}[X\vert\mathcal{B}]$.
- (Taking out) If $Z$ is measurable by $\mathcal{A}$, then $\mathbb{E}[XZ\vert\mathcal{A}] = Z\mathbb{E}[X\vert\mathcal{A}]$.
- (Independence) If $\mathcal{B}$ is indepenent with $\sigma(X,\mathcal{A})$, then $\mathbb{E}[X\vert\sigma(\mathcal{A},\mathcal{B})] = \mathbb{E}[X\vert\mathcal{A}]$.
- (Chebyshev) $q>0$, $\mathbb{E}[\lvert X\rvert^q] < \infty$, then $\mathbb{P}[\lvert X\rvert \ge \varepsilon \vert\mathcal{A}] \le \varepsilon^{-q}\mathbb{E}[\lvert X\rvert ^q\vert\mathcal{A}]$.
- (Jensen) For all convex function $\varphi:\mathbb{R}\to\mathbb{R}$, we have $\varphi(\mathbb{E}[X\vert\mathcal{A}]) \le \mathbb{E}[\varphi(X)\vert\mathcal{A}]$.
- (Holder) Set $p,q>1$ with $p^{-1}+q^{-1} = 1$, $X\in L^p$ while $Y\in L^q$, then $\mathbb{E}[\lvert XY\rvert \vert \mathcal{A}] \le (\mathbb{E}[\lvert X\rvert ^p\vert\mathcal{A}])^{1/p}(\mathbb{E}[\lvert Y\rvert ^q\vert\mathcal{A}])^{1/q}$.
Prop. 若随机变量$Z$是$\sigma(X)$可测的, 则存在Borel可测函数$h$使得 $Z = h(X)$.
Prop. $\mathbb{E}[Y\vert X] = h(X) \Leftrightarrow \forall f \in BrB, \mathbb{E}[Yf(X)] = \mathbb{E}[g(X)f(X)]$.
Prop. $(X,Z_1,\cdots,Z_n)$ 是一个Gauss随机变量, 均值为0, 则存在一系列实数$a_i$使得 $\mathbb{E}[X\vert Z_1,Z_2,\cdots,Z_n] = \sum_{i=1}^n a_iZ_i$.
Martingale
Def. (Martingale) $\mathfrak{X} = \{X_n\}_{n\in \mathbb{N}_0}$ is an $\mathbb{F}$-Martingale, if
- $X_n \in L^1(\Omega, F, \mathbb{P})$;
- $X_n$ is $F_n$-measurable ($\mathfrak{X}$ is adapted to $\mathbb{F}$)
- For all \(m \le n \in \mathbb{N}_0,\) we have \(\mathbb{E}[X_n \vert F_n] = X_m\). Equivalently, \(\mathbb{E}[X_{n+1}\vert F_n] = X_n.\)
And we define sub-martingale and super-martingale for $\ge$ and $\le$ case.
L’evy Martingale: $X_n = \mathbb{E}[Y\vert F_n]$.
Stopping Time
A random variable $\tau: \Omega\to \mathbb{N}^*$ is a $\mathbb{F}$-stopping time, if $\{\tau = n\} \in F_n, \forall n\in \mathbb{N}_0$. Alternative condition: $\{\tau \le n, \tau > n\}$.
Def. (Stopped $\sigma$-Algebra) $F_\tau = \{A\in F: A\cap \{\tau = n\} \in F_n, \forall n\in \mathbb{N}_0\}.$ Properties:
- $F_\tau \subset F$ as a sub sigma-algebra; and if $\tau = k$ is a constant, we have $F_\tau = F_k$.
- If $\sigma\le \tau$, then $F_\sigma \le F_\tau$; $F_{\tau \wedge \sigma} = F_\tau \cap F_\sigma$.
Define
\[X_\tau = \sum_{l=0}^\infty X_l(w)\mathbf{1}_{\tau = l} + X_\infty\mathbf{1}_{\tau = \infty}, X_n^\tau = X_{\tau \wedge n}, \mathfrak{X}^\tau = \{X_n^\tau\}_{n\in \mathbb{N}_0}.\]Then $X_\tau, X_n^\tau$ are $F_\tau$-measurable.
Thm. (Stability upon stopping) If $\{X_n\}_{n\in \mathbb{N}_0}$ is an F-martingale, then $\{X_n^\tau\}$ is for all F-stopping time $\tau$.
Thm. (Doob’s optional sampling) $\tau,\sigma$ are $F$-stopping times, \(\tau \le \sigma \le N \in \mathbb{N}_0 \Rightarrow \mathbb{E}[X_\tau \vert F_\sigma] = X_\sigma.\)
Cor. $\mathbb{E}[X_\tau] = \mathbb{E}[X_0]$ happens in the following cases:
- Bounded stopping time $\tau \le N$.
- $L^1$ dominated: $\lvert X_n\rvert \le Y \in L^1$ $\mathbb{P}$-a.s., and $\mathbb{P}[\tau = \infty] = 0$.
- Bounded increment: $\lvert X_{n+1}-X_n\rvert \le M$ $\mathbb{P}$-a.s., and $\mathbb{E}[\tau] < \infty$.
- Nonnegative supermartingale.
Convergence Theorems
对于一个鞅 $\mathfrak{X}$, 我们思考当 $n\to \infty$ 时 $X_n$ 的收敛情况: 首先, 定义 $F_{\infty}$ = $\sigma(\cup_{n}F_n)$, 若存在 $X_\infty$ 满足是 $F_\infty$ 可测的, 而且 $\mathbb{E}[X_n\vert F_m] = X_m$, 则我们称$X_\infty$为这个鞅的终元.
Thm. (SuperMartingale Convergence Theorem) 设 $X$ 是一个上鞅, 并且 $M = \sup_{n\in\mathbb{N}_0}\mathbb{E}[(X_n)]<\infty$,
则存在 $X_\infty$ 是 $F_\infty$ 可测的, 且 $X_n$ 几乎处处收敛到 $X_{\infty}$; 若这是一个非负上鞅, 则 $X_\infty$ 也是终元.
Lemma. $X\in L^1(\Omega)$, 则 $X_t = \mathbb{E}[X\vert F_t]$ 是一致可积的.
Thm. 若$\mathfrak{X}$是一个F鞅, 则以下命题等价:
- $\mathfrak{X}$ 一致可积;
- 存在 $X_\infty \in L^1$, 使得$X_n$几乎处处收敛到$X_\infty$; (由一致可积性可知也有$X_n$依$L^1$范数收敛到$X_\infty$).
- $\mathfrak{X}$ 是一个Levy鞅. (此时恰有$X_n = \mathbb{E}[X_\infty\vert F_n]$, 从而$X_\infty$是终元)
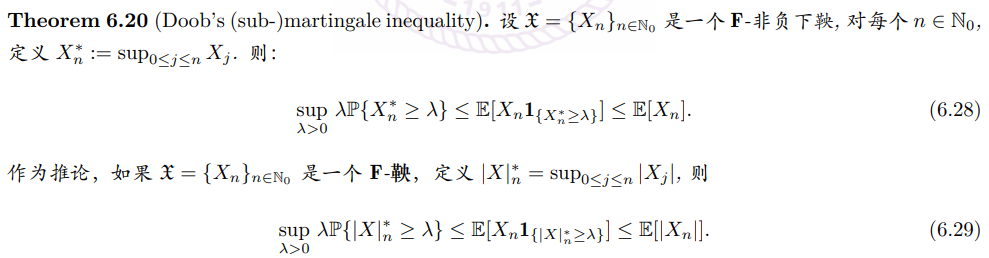
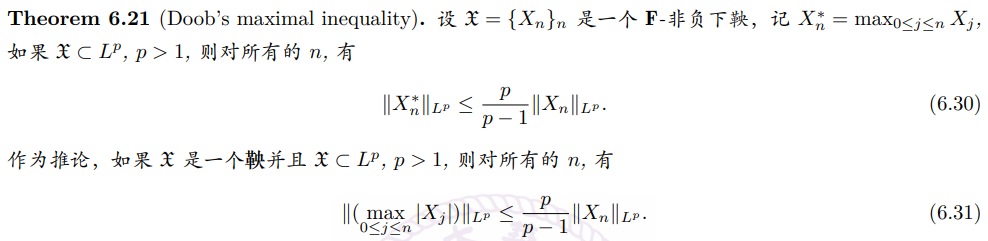
Thm. 若$\mathfrak{X}$是一个F鞅, 且$\mathfrak{X}\subset L^p$, 则以下命题等价:
- $\mathfrak{X}$ 在 $L^p$ 中有界, 即 $\sup \lVert X_n\rVert_{L^p}<\infty$;
- 存在 $X_\infty \in L^p$, 使得 $X_n$ 几乎处处收敛到 $X_\infty$, 且 $X_n$ 依 $L^p$ 范数收敛到 $X_\infty$.
- $\mathfrak{X}$ 是一个Levy鞅. (此时恰有 $X_n = \mathbb{E}[X_\infty\vert F_n]$, 从而 $X_\infty\in L^p$ 是终元)
Chapter 7: Markov Chain
Def. (Markov Property) $\mathbb{P}\{X_{n+1}\in B \vert F_n\} = \mathbb{P}\{X_{n+1}\in B\vert X_0,X_1,\cdots ,X_n\} = \mathbb{P}\{X_{n+1}\in B \vert X_n\}, \forall n\in \mathbb{N}_0, \forall B\in \mathcal{B}(\mathbb{R})$
This is equivalent to $\mathbb{P}\{A\cap B \vert F_{\{n\}}\} = \mathbb{P}\{A\vert F_{\{n\}}\}\mathbb{P}\{B\vert F_{\{n\}}\},\forall A\in F_{[n+1,\infty)},B \in F_{[0,n]}.$
时间平稳性(time-homogeneous):$\mathbb{P}\{X_{n+1}\in B \vert X_n = s\}$ 均不依赖于 $n$.
这时对可数状态空间,我们有状态转移矩阵 $P(i,j) = \mathbb{P} \{ X_{n+1} = j \vert X_n = i \}$, 满足 $\sum_{j \in S}P(i,j) = 1, \forall i \in S$.
有以下结论:
\[\mathbb{P}[(X_0,X_1,\cdots, X_n) = (x_0,x_1,\cdots x_n)] = P(x_{n-1},x_n)P(x_{n-2},x_{n-1})\cdots P(x_0,x_1) \mu_0(x_0) \\ \mathbb{E} [f(X_{n+1}) \vert X_0,X_1,\cdots,X_n] = \mathbb{E}[f(X_{n+1})\vert X_n] = (Pf)(X_n), (Pf)(x) := \sum_{y\in S} P(x,y)f(y).\]稳态分布(stationary distribution): $\pi = \pi P$, i.e., $\pi(y) = \sum_{x\in S}P(x,y)\pi(x), \forall y \in S$.
常返性(Recurrency)和瞬变性(Transiency)
Prop. (Strong Markov Property) If $\{X_n\}_{n\in N_0}$ has transition matrix $P$, $\tau$ is a $\mathbb{F}-$stopping time, $F = \sigma(X_0,X_1,\cdots,X_n)$, then $\forall \mu_0, G \in \mathcal{S}^\infty$, we have
\[\mathbb{P}_\mu [(X_{\tau+1},X_{\tau+2}, \cdots) \in G \vert F_\tau] = \mathbb{P}_{X_\tau} [(X_1,X_2,\cdots)\in G] \ \mathbb{P}\text{-a.s. on } \{\tau < \infty\}.\]Thm. (Dichotomy of recurrency)
- (Recurrent)
- (Transient)
Def. 对于常返的 $j\in S$, 我们还可以定义 $j$ 是正常返的, 如果 $\mathbb{E}_j[\tau_j^+] <\infty$; 否则 $\mathbb{E}_j[\tau_j^+] = \infty$ 为零常返的.
不可约性
Def. 若从 $x$ 出发在有限时间内到达 $y$ 的概率 $\rho(x,y)>0$, 则称 $y$ 是 $x$ 的可达态, 记作$x\to y$; 若 $S$ 中的任意两个元素两两可达, 则称 $(S,P)$ 是不可约的.
Def. 记 $R(x) = \{n\ge 1: P^n(x,x) > 0\}$, 则 $\gcd R(x)$ 称为马氏链的周期; 对于不可约马氏链, 在任意点处定义的周期都是一致的. 若 $\gcd R(x) =1$ 则称之为非周期的.
定义一个停时 $T_y^k = \inf\{n>T_y^{k-1}: X_n = y\}$ 表示第 $k$ 次到达 $y$ 的时间. 我们有 $\mathbb{P}[T_y^k < \infty] = \rho(x,y)(\rho(y,y))^{k-1}$. 再记 $N(y) = \sum_{n=1}^\infty \mathbf{1}_{X_n(\omega) = y}$, 即从 $x$ 出发的路径经过 $y$ 的次数, 则 \(\mathbb{E}[N(y)] = \begin{cases} \frac{\rho(x,y)}{1-\rho(y,y)}, &\rho(x,y) > 0 \\ 0, &\rho(x,y) = 0\end{cases}.\)
因此 $x$ 是常返态等价于 $\mathbb{E}_x [N(x)] = \infty$, 或是 $\mathbb{P}_x[N(x) = \infty] = 1$.
Thm. 对于不可约的马氏链, 若有一点常返则每一点均为常返, 且从任何一点出发都几乎必然无限次经过其他所有点. 即
\[\exists x \in S, \rho(x,x) = \mathbb{P}_x[T_x < \infty] = 1 \Leftrightarrow \forall x,y\in S, \rho(x,y) = \mathbb{P}_x[T_y <\infty] = 1.\]Thm. 若 $S$ 有限不可约, 则 $S$ 至少有一个常返态, 从而每一点均为常返的.
Thm. 若 $S$ 不可约, 则 $\exists x\in S, \mathbb{E}_x[T_x] < \infty \Leftrightarrow \forall x,y\in S, \mathbb{E}_x[T_y]<\infty$. (此时$S$是正常返的)
Thm. 若 $S$ 不可约, 则 $S$ 正常返当且仅当存在唯一的稳态分布.